Calculating triangular arbitrage lot size for a perfectly hedged triangular arbitrage ring is straightforward once you understand the simple math behind the prices. To get started you need three related pairs that form a ring or triangle, and simultaneous prices from those three pairs.
In a previous article a triangular arbitrage example was designed using three currency pairs and their simultaneous prices. In this article we will use the following ring and prices to work a series of examples showing how to compute the fully hedged lot size for a triangular arbitrage ring:
EURUSD = 1.4169 GBPUSD = 1.60655 EURGBP = 0.8821
It was shown that when you have the prices for three currency pairs, it is trivial to determine which pair is out of balance, or in other words, which pairs are overvalued and which are undervalued relative to the triangular arbitrage ring. Knowing which pair is relatively high and which is relatively low is important if you wish to execute a triangular arbitrage ring in the proper direction to capture the inefficiency, as shown in the picture below.
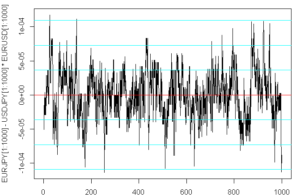
The picture shows an example view of a triangular arbitrage inefficiency in EURJPY – USDJPY * EURUSD over 1000 bid ask price changes (a very short period of time). It is apparent that there is persistent but very small inefficiency apparent between the markets – only about 1 scaled pip or 0.0001 at the 3 standard deviation level. In a general sense, you can determine which pair is out of balance by the following three formulas computed from the EURUSD, GBPUSD and EURGBP data previously stated:
EURUSD-EURGBP*GBPUSD = 1.4169 - 0.8821 * 1.60655 = EURUSD overvalued by 0.00024 EURGBP-EURUSD/GBPUSD = 0.8821 - 1.4169 / 1.60655 = EURGBP undervalued by -0.00015 GBPUSD-EURUSD/EURGBP = 1.60655 - 1.4169 / 0.8821 = GBPUSD undervalued by -0.00027
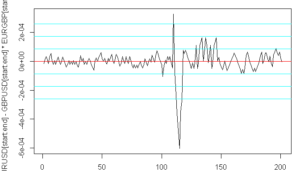
The picture below shows what a 6.9 sigma jump looks like with EURUSD – GBPUSD*EURGBP. The absolute move is only 6 pips away from parity and is only identifiable with bid / ask data. Can you execute the arb quick enough to capture the 6 pips less trading costs and spread?
But what do you do if you want to size your positions to form a perfect hedge? How do you calculate the correct lot size for a fully hedged triangular arbitrage ring? First you need to select a pair from the ring and select an initial lot size. I’ll select EURUSD and a lot size of 10,000 units.
To break down exposure of the EUR/USD pair when you buy 10,000 EUR/USD you own 10,000 EUR and in order to finance the purchase of EUR you must borrow an equivalent amount of USD. To work out the quantity of USD, simply multiply by the exchange rate.
The sign for USD is negative because when you go long EUR you are short USD as in EUR/USD. Likewise when you go short EUR, you are long USD.
Buy 10,000 EUR/USD = +10,000 EUR - 14,169 USD (-10,000 * 1.4169)
The sign for USD is negative because when you go long EUR you are short USD as in EUR/USD. Likewise when you go short EUR, you are long USD.
If you wished to initiate a ring where you buy 10,000 EURUSD it is possible to work out the other exposures as such:
EUR/USD long 10,000: EUR + 10,000, USD -14,169. Take the USD and impute the amount of GBP as follows: GBP/USD short 14,169 / 1.60655 = short 8,820 (rounded) GBP which comes out to 8820 x 1.60655 = 14,170 USD long (rounded). EUR/GBP short sell 10,000 to offset the existing 10,000 long EUR which comes out in GBP as 10,000 * .8821 = 8821 GBP long
So to summarize:
1.4169 EUR/USD long 10,000 EUR, short 14,169 USD 1.60655 GBP/USD short 8,820 GBP, long 14,170 USD 0.8821 EUR/GBP short 10,000 EUR, long 8,821 GBP
To work out how well the exposure has cancelled we can compute:
EUR: 10,000 - 10,000 = 0 EUR residual exposure GBP: -8820 + 8821 = 1 GBP residual exposure USD: -14169 + 14170 = 1 USD residual exposure
All but 1 GBP and 1 USD was cancelled. In like manner starting with either of the other two pairs, the same set of equations can be worked out summarized as follows: (where + is long and – is short)
1.60655 GBP/USD +10,000 = GBP + 10,000, USD -16,066 0.8821 EUR/GBP -10,000 GBP and imputed 10,000 /0.8821 = +11,337 EUR 1.4169 EUR/USD -11,337 EUR, +16,063 USD
Residuals are -3 USD. Finally:
0.8821 EUR/GBP -10,000 EUR, + 10,000*0.8821 = +8821 GBP 1.60655 GBP/USD -8821 GBP, +8821 * 1.60655 = +14,171 USD 1.4169 EUR/USD +10,000 EUR, 10,000*1.4169 = -14,169 USD
Residuals are -2 USD.
There may be some fractional residuals that are not accounted in this analysis but for practical purposes small residuals can be ignored as they are too small to affect a trader’s equity much due to the very small size.
Also, from a practical standpoint many forex brokers enforce a minimum size that makes much of the discussion on size moot. Sizes on mini lot brokers that offer 0.01 lot sizing are minimum of 100 units so rounding of lot sizes would need be done at that level. Standard lot brokers offering 0.01 lot sizing would round to the nearest 1000 units.
So there you have it, three ways to compute the hedged lot size to use for triangular arbitrage. You can start with any of the three currency pairs within the triangular arbitrage ring with a desired size and then by following the pattern in the examples above, you can calculate the other correct lot sizes for the entire triangular arbitrage ring. Work through the examples above on your own (or some of your own choosing) to make sure you understand how to work the math. You need the current prices for all three pairs so the easiest way to record the prices before they change is to take a screen shot.
If you need a review of the basics of Triangular Arbitrage, or wish to be able to determine which pairs in a ring are out of balance and by how much, take a look at the article titled The basics of Triangular Arbitrage. For more advanced topics, take a look at Triangular Arbitrage with Bid and Ask Quotes.
![]()

