Triangular arbitrage involves placing offsetting transactions in three forex currencies to exploit a market inefficiency for a theoretical risk free trade. In practice, there is substantial execution risk in employing a triangular arbitrage or tri arb strategy which may make it difficult to profit for retail traders. However, a knowledge of triangular arbitrage mechanics can enable forex traders to understand better how market prices self-regulate.
In addition, this understanding may lead to strategy development that may be exploited by the retail trader, peeking into the realm of statistical arbitrage. The concept of triangular arbitrage is related to but distinct from stat arb or pairs trading, which may deal with two or more currency pairs.
On a retail forex level, currency prices are quoted in currency pairs. This is significant because a single forex transaction actually includes two currencies in one rate. A retail forex trader doesn’t actually buy or sell any physical currency, but rather buys or sells a cross rate which is supposed to represent the cost to buy or sell from one currency to another. In practice, because no physical currency changes hands, trading a currency pair is similar to trading a stock or any other financial instrument where the quoted price is executable and profit or loss is determined by appreciation of the instrument after purchase or depreciation of the instrument after sale minus transaction and carry costs.
Triangular Arbitrage Example
An example of a triangular arbitrage ring is U.S. dollar (USD), British pound (GBP), and Euro (EUR). The currency pairs involved in such an arbitrage opportunity are EUR/USD, GBP/USD and EUR/GBP. Note that these pairs can be thought of as an algebraic formula with a numerator and a denominator. The numerator in EUR/USD is the Euro or EUR, while the denominator in that pair is the U.S. dollar (USD). This equation works out to EUR divided by USD. These three currency pairs make up a tri arb ring.
Synthetic Pairs
Using the triangular arbitrage formula it is possible to create synthetic currency pairs from the other two pairs in a ring. For example EUR/USD = GBP/USD * EUR/GBP. Recall from basic algebra that when two fractions are multiplied, identical diagonal values can be crossed out or eliminated. In this case GBP is in the numerator of the GBP/USD pair, and GBP is in the denominator of the EUR/GBP pair. When these two pairs are multiplied, the GBP in the numerator cancels out the GBP in the denominator and EUR/USD is left, so the equation resolves to EUR/USD = . (The GBP in parentheses cancel out).(GBP)/USD * EUR/(GBP) = EUR/USD
To finish out this particular ring, synthetic pairs can also be created for GBP/USD and for EUR/GBP. GBP/USD = GBP/. There is no pair for GBP/EUR so the pair EUR/GBP is mathematically inverted by dividing 1 by the pair as so: EUR * EUR/USDGBP/EUR = 1/(EUR/GBP). In this example the EUR in the denominator and in the numerators cancel each other out and the formula leaves GBP/USD = GBP/.(EUR) * (EUR)/USD = GBP/USD
The third formula is EUR/GBP = EUR/. Again, there is no USD/GBP so GBP/USD is inverted by taking 1 and dividing it by the pair as USD * USD/GBPEUR/GBP = EUR/. Fractions in the denominator are inverted and multiplied, leaving (USD) * 1/[GBP/(USD)]EUR/.(USD) * (USD)/GBP = EUR/GBP
In this way it is possible to create a synthetic pair out of a valid triangle or ring for each of the underlying pairs. To recap the synthetic pairs:
EUR/USD = EUR/GBP*GBP/USDGBP/USD = GBP/EUR*EUR/USDEUR/GBP = EUR/USD*USD/GBP
To create the formula for triangular arbitrage with a mean centered at zero, it is merely necessary to get all the terms on the correct side of the equation.
EUR/USD - EUR/GBP * GBP/USD = 0alternatively this can be written as follows:
log(EUR/USD) - log(EUR/GBP) - log(GBP/USD) = 0See graphics below to illustrate that both formulas written above produce identical results.
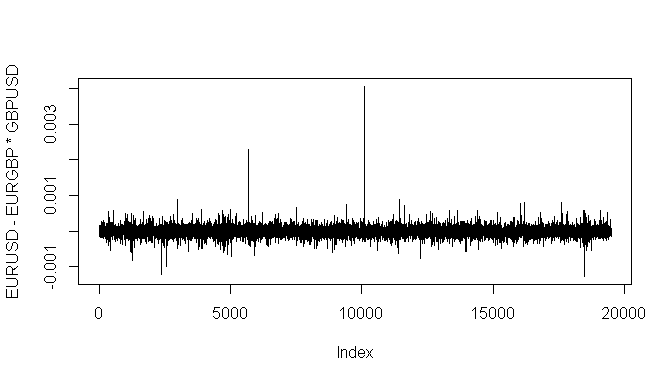
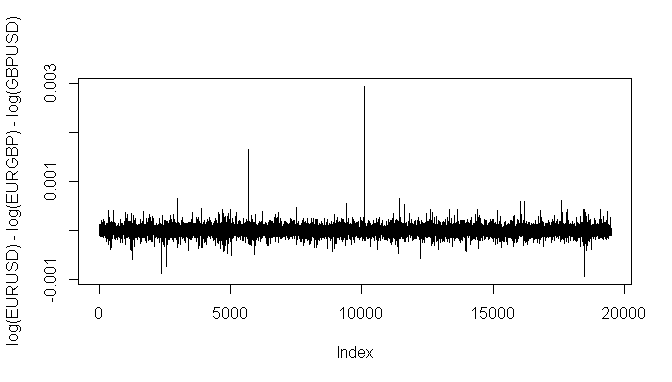
A practical approach
If this formula is plotted you will note that it roughly centers around zero but at times has serious excursions from this value. Playing the deviations for reversion is a game of the quickest of the quick and really isn’t an achievable aim for retail forex traders who trade through a forex dealer (also known as a market maker or bucket shop). Attempting this type of triangular arbitrage on retail forex brokers is generally discouraged in customer agreements and will typically lead to the broker implementing countermeasures of increased slippage, slow fill times and sometimes no fill at all. Because this type of “risk free” tri arb is extremely time sensitive, even a small delay in order placement is enough to nullify any potential profit. Profits from a triangular arbitrage strategy are small but consistent to those who are quickest to spot and act on the imbalance.
But it is worth noting that inherent in practical Triangular Arbitrage is significant execution risk, a glaring problem with the practical implementation of this “risk free” strategy. There may be some opportunities available on forex ECNs, however this remains a game of the quickest so latency and colocation play a large part in determining who profits from triangular arbitrage opportunities.
Calculation Example
An example using three prices follows:
EURUSD = 1.4169 GBPUSD = 1.60655 EURGBP = 0.8821
Using the formula above (EUR/USD -EUR/GBP * GBP/USD = 0) we have:
1.4169 - 0.8821 * 1.60655 = 0 which simplifies to -0.000237755 = 0.
Clearly a small discrepancy exists between the theoretical equilibrium price of zero and the actual price of -0.00024 (rounded). However, because three pairs are involved the 2.4 pips discrepancy may not be able to be overcome if all three pairs are transacted for a supposed risk-free transaction. As buyers come into one market and bid and take offers, that currency pair is pushed out of balance with the others. The currency pair may come back into balance in one of two basic ways. Either the currency pair that is out of balance can be arbitraged back into balance, or one or both of the other two pairs can be arbitraged to bring balance back to the triad.
Which Pair is Out of Balance?
A common question is to wonder how to tell which pair is out of balance in a triangular arbitrage situation? One possible solution is to consider the synthetic pairs that make up the tri arb.
We know that EUR/USD = EUR/…GBP * GBP/USD
When the numbers are worked out, we conclude that 1.4169 < 1.417138, or that the EUR/USD (1.4169) is priced lower than the synthetic EUR/USD (1.417138). This may indicate that EUR/USD is underpriced relative to the other two pairs. Note that out of balance does not automatically mean that future re-balancing will lead to EUR/USD price rising though it may lead to EUR/USD being bought by arbitrageurs. It is also possible if there is sufficient supply of EUR/USD for prices to continue to drop relative to the others or to not rise as quickly (in an uptrend), but that the other two pairs catch up with the under-valued EUR/USD to keep the triangle in balance. Working out the other two synthetic currency pairs we see that…
GBP/USD = GBP/EUR * EUR/USD or 1.60655 > 1.60628.In this case GBP/USD is higher priced than its synthetic. And finally:
EUR/GBP = EUR/USD * USD/GBP or 0.8821 > 0.881952...…indicating that EUR/GBP is also priced higher than its synthetic.
Summary
In summary it is apparent that EUR/USD is lower priced than its synthetic currency pair, while both GBP/USD and EUR/GBP are higher priced than their synthetic currency pairs. Making the assumption that the synthetic currency pairs represent true or actual value, it would then be apparent that:
EUR/USD is under valued 1.4169 – 1.417138 = -0.00024 or -2.4 pips
GBP/USD is over valued 1.60655 – 1.60628 = +0.00027 or +2.7 pips
EUR/GBP is over valued by 0.8821 – 0.881952 = +0.000148 or + 1.48 pips
Thus if a triangular arbitrage trade were initiated to revert to the zero mean, EUR/USD would be bought, while GBP/USD and EUR/GBP would be sold. After inspecting the magnitude of the discrepancy, it is clear that GBPUSD is more out of balance than the other two pairs (though only slightly more than EURUSD is out of balance), so it may be that GBP/USD will be first to be arbed back into line. Or it may be that GBP/USD is most vulnerable to a mean reversion to bring the triad back into line.
It must be remembered that the prices in the above illustration are not bid/ask prices and as such the perceived opportunity may be much smaller (or non-existent) than described. The next question to answer relates to the size of each currency pair to trade. The initial instinct might indicate that equal sizes would balance out against each other, but that is not correct. More on lot sizes and recreating the arbitrage ring using bid and ask prices in future posts.
![]()


thank you very much for clarification